26. 10 .2020r.
Temat: Cechy podzielności liczb przez 2, 5, 4, 10 i 100 oraz przez 9 i 3.
Witajcie. Na ostatniej lekcji zapisaliśmy cechy podzielności przez 2, 5, 4, 10 i 100 oraz przez 9 i 3. Na dzisiejszych zajęciach będziemy stosować poznaną wiedzę w zadaniach. Na początku przyjżyjmy się jescze raz poszczególnym cechom umieszczonym na planszach: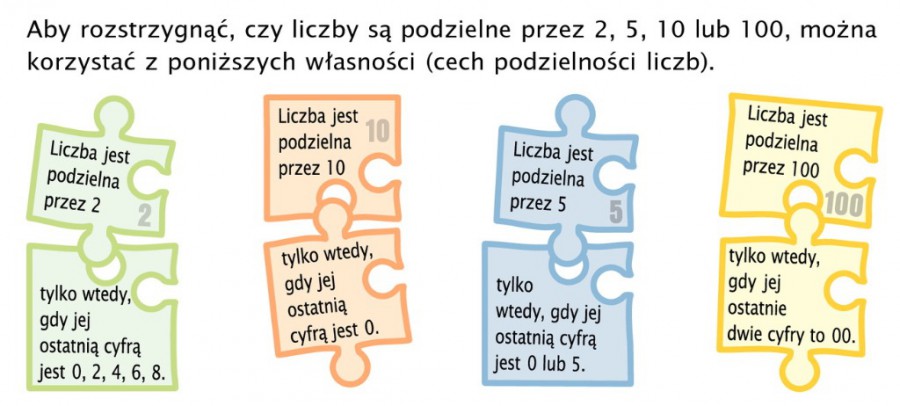


Następnie do zeszytu przepiszmy przykład z zadania 1
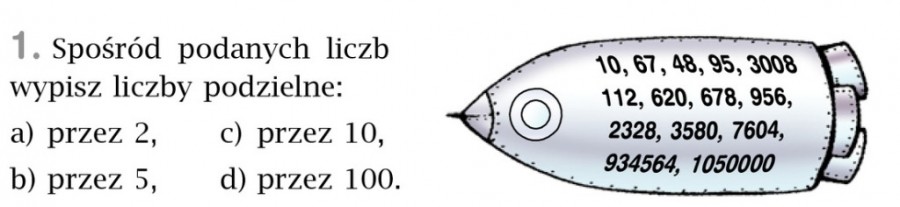
Przez 2: 10, 48, 3008, 112, 620,678, 956, 2328, 3580, 7604, 934564, 1050000; (te liczby, których ostatnią cyfrą jest 0, 2 4, 6, 8)
Przez 5: 95, 10, 620, 3580,1050000 (te liczby, których ostatnią cyfrą jest 0 lub 5)
Przez 10:10, 620, 3580,1050000 (ostatnią cyfrą jest 0)
Przez 100: 1050000 (dwiema ostatnimi cyframi są zera)
Przez 4: 48, 3008, 112, 620, 2328, 3580, 7604, 934564, 1050000 (Patrzymy na dwie ostatnie cyfry. Tworzą one liczbę podzielną przez 4)
Przez 3: 48 (4+8=12, 12:3=4), 678 (6+7+8=21, 21:3=7), 2328 (2+3+2+8=15, 15:3=5), 1050000 (1+5=6, 6:3=2)
Przez 9: Nie ma takiej liczby.
Zadanie. Do śrosy 28.10.2020 wykonaj zadania w zeszycie ćwiczeń 1-8 str 19-20. Zdjęcia zadań prześlij na adres siwikp@wp.pl
28. 10.2020r
Temat: Liczby pierwsze i liczby złożone.
Witajcie. W trakcie ostatnich lekcji poznaliśmy metodę znajdywania dzielników liczb i poznaliśmy cechy podzielności liczb przez 2, 5, 10, 100, 4, 3 i 9. Przeanalizujmy sobie następujący przykład, który wpiszecie do zeszytu:
Przykład 1:
Liczba 4 posiada 3 dzielniki: 1, 2 i 4;
Liczba 6 posiada 4 dzielniki: 1, 2, 3 i 6
Liczba 12 posiada 6 dzielników: 1, 2, 3, 4, 6 i 12;
Liczba 13 posiada tylko 2 dzielniki: 1 i 13. Takich liczb jak 13 jest znacznie więcej, są to: 5, 7, 11, 13,17, 19, 23 itd. O takich liczbach, które posiadają tylko 2 dzielniki mówimy, że są to liczby pierwsze. Pozostałe liczby, które maja tych dzielników więcej nazywamy złożonymi. Zatem zapiszcie w zeszycie poniższą ramkę:


Następnie w zeszycie rozwiąż poniższe zadanie:
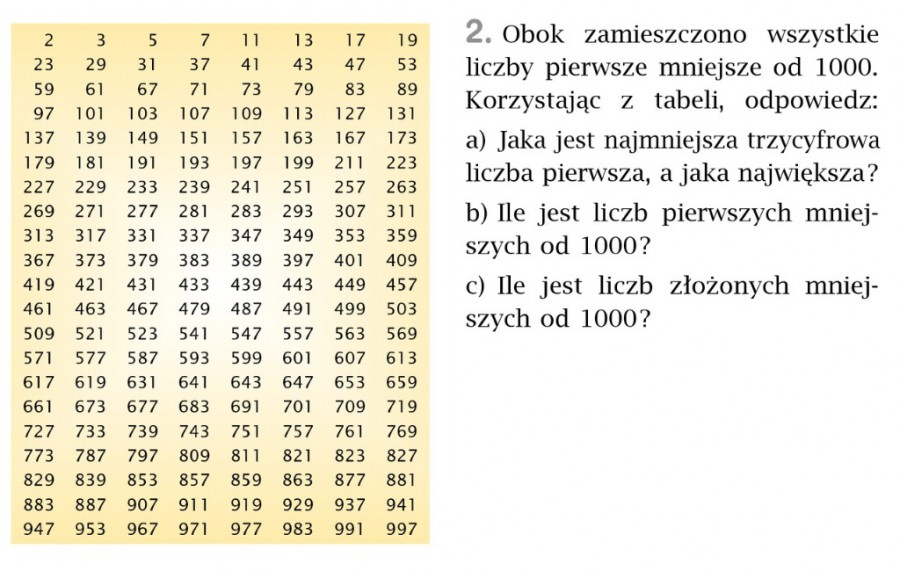
30.10.2020r
Temat: Rozkład liczby na czynniki pierwsze.
Wiemy z poprzedniej lekcji co to jest liczba piewrwsza - taka licza, która dzieli się jedynie przez samą siebie i przez liczbę 1. Oczywiście pamiętamy, że 0 i 1 nie są liczbami ani pierwszymi ani złożonymi. Dziś naiczymy się rozkładać liczbę na czynniki pierwsze - co to oznacza?
Weźmy liczbę 12. Możemy ją ozłożyć na iloczyn 12=2*6, ale ktos sprytny powie, że liczbę 6 możemy również rozłożyć na iloczyn 12=2*2*3. Zauważcie, że tego iloczynu nie da się dalej rozłożyć, co określamy w matematyce, że rozłożyliśmy liczbę 12 na czynniki pierwsze (zauważcie - liczby 2 i 3 są liczbami pierwszymi). Oczywiśćie bardzo łatwo możemy rozkładać małe liczby, trudniej jest rozkładać duże liczby. Posługujemy się wówczas pewnym algorytmem (sposobem), który nam taki rozkład wyznaczy:
W tym celu obejrzyj filmik, który jest TUTAJ
Następnie spróbuj wyznaczyć rozkłady na czynniki pierwsze liczb: 112, 50, 75, 42, 36, 642. Rozwiązania prześlij na moją pocztę siwikp@wp.pl do wtorku 02.11.2020